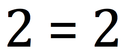Laboratory Fractions can be difficult to learn. As the joke goes, “Three out of every two people have trouble with fractions”. This can be especially true for primary school children. So, what is so special about fractions? Why are they harder to learn than other numbers, such as integers?
We Wondered
When people use fractions, we wondered whether their brains are processing their local or global values. Let me explain. When you look at a whole number, such as the number 2, there is only one value that is being represented (i.e. the value of 2 is 2).

We Put it to the Test
We conducted a study with adult volunteers1. We showed them two fractions and asked them to decide as quickly as possible whether they represented the same magnitude or not (this is known as a same/different task). Fractions which were equivalent in global value (e.g. 1/4 and 2/8) were only correctly identified as representing the same number about half of the time. This helps to confirm that people tend to have trouble with fractions.
In another experiment, we again showed a pair of fractions to adult participants, but this time we asked them to decide which of two fractions was larger (a comparison task). The results of this experiment went further than just confirming that fractions are difficult to work with. The data from this experiment suggested that participants processed fractions differently depending on how simple the fraction was. For easy (or very familiar) fractions, they relied mostly on the global value of the fraction to compare it to others. With more difficult (or less familiar) fractions, they used the local values of the numerator and denominator.
What About Children?
Do children process fractions in the same way as adults? We gave the same two tasks described above to children in years 5, 6, and 72. In the same / different task, all three groups of children relied only on the local values of fractions. In the number comparison task, the year 5 pupils used local values only; however, beginning with year 6 and continuing through year 7, students developed the ability to use the global value for easier fractions, similarly to adults.
So Why Are Fractions Harder to Learn?
One of the purposes of our study was to find out whether or not people have an innate (i.e. born with) ability to process fractions using their global value. Our studies with children show that this is not likely since the youngest (Year 5) children did not use global values at all and the Year 6 & 7 children only seemed to use them for comparison, most probably because of what they were being taught in school.
It could be that one of the the things that makes fractions more difficult to work with are their multiple values. When the brain deals with fractions it has to deal with at least two local values as well as a global value. When dealing with other integers, such as whole numbers, there is only one value to process.
References
1) Gabriel, F., Szűcs, D., & Content, A. (2013). The mental representations of fractions: Adults' same–different judgments. Frontiers in Cognition, 4, 385. https://doi.org/10.3389/fpsyg.2013.00385
2) Gabriel, F., Szűcs, D., & Content, A. (2013). The Development of the Mental Representation of Fraction Magnitude. PLOS ONE, 8(11), e80016. https://doi.org/10.1371/journal.pone.0080016
Further Reading
Bright, G., Bear, M., Post, T. R., & Wachsmuth, I. (1988). Identifying Fractions on Number Lines. Journal for Research in Mathematics Education, 19(3), 215-232.
Mamede, E., Nunes, T., & Bryant, P. (2005). The equivalence and ordering of fractions in part-whole and quotient situations. Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education, 3.