The PSI was originally devised to quantify the phase synchronization between two oscillators of different frequencies (e.g., muscle activity; Tass et al., 1998). It was subsequently adapted for use in neural analyses of oscillatory phase-locking (e.g., Schack & Weiss, 2005). In this analysis, PSI is used to measure the degree of temporal synchronisation (phase locking) between pairs of speech AMs at different timescales (i.e. Stress:Syllable and Syllable:Phoneme).
The relationship between the frequencies of AMs is described by the ratio n:m, where n and m are integers. The degree of synchronisation is calculated by the PSI which is defined as :
where θ1 and θ2 are the instantaneous phases of the oscillations being compared. In Eq. (1), the PSI is the magnitude of the average difference in the phase angles. PSI can range from 0 (no synchronisation) to 1 (complete synchronisation).
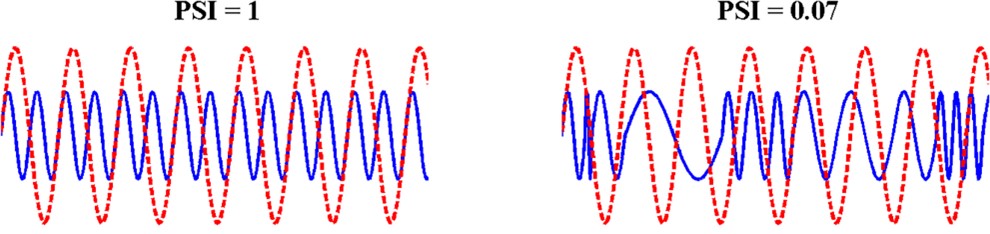
Figure 2. Hypothetical amplitude modulation (AM) pairs (sinusoids) that yield Phase Synchronization Index (PSI) scores of 1 (left) and 0.07 (right), respectively. The red and blue curves represent AMs with a frequency ratio of 1:2. From Leong et al (2017) The Temporal Modulation Structure of Infant-Directed Speech. Open Mind. 1(2):78-90. doi:10.1162/OPMI_a_00008
The n:m ratio for Stress:Syllable and Syllable:Phoneme AMs were determined to be 1:2 and 1:3 respectively for English nursery rhymes (Leong and Goswami, 2014). The same ratios were also found to be optimal in Portuguese (Arajo et al, 2018). In Spanish child directed speech (CDS), Perez-Navarro et al., found n:m ratios of 1:2 to be optimal for Stress:Syllable AMs (Perez-Navarro et al., In review). The Syllable:Phoneme AMs are currently under investigation (Perez-Navarro et al., unpublished research). The optimal n:m ratio for other languages are still to be investigated.
The MATLAB code to compute the PSI between AMs for each frequency band can be found HERE